1. Array - CAtlArray, CArray, std::vector
C언어에서 지원하는 배열과 똑같은 문법으로 사용할 수 있는 말그대로 배열이다. 단, 그 크기가 동적으로 변할 수 있다. C언어의 배열과 같이 operator[]로 접근이 가능하다. 즉, random access가 가능하다. 가장 가벼운 오버헤드를 가지고 있고, 단순한 자료 저장은 최대한 배열을 사용해야한다.
- 삽입/삭제: 배열 끝에서의 추가 및 삭제는 상수 시간 O(1). 그러나 그 외의 원소를 삽입/삭제 할 경우에는 O(n)의 시간이 걸린다. 여기서 잠깐 알고리즘 수행 시간(time complexity)을 나타내는데 쓰이는 Big-Oh notation에 대해서 알아보자:
- O(1): 현재 배열의 크기와 상관없이 언제나 같은 시간이 걸린다는 뜻이다. 배열 마지막에 새로운 원소를 넣는 작업의 경우, 배열의 크기를 알고 있기 때문에 for 순환 없이 바로 작업을 수행할 수 있다.
- O(n): 주어진 작업을 완료하기 위해서는 최악의 경우, 현재 배열의 길이만큼 탐색을 해야한다. 정렬되지 않은 배열에서 특정 원소를 찾는 것은 최악의 경우 모든 원소를 다 뒤져 봐야하므로 배열의 길이에 비례하는 시간이 걸린다.
- O(log n): 만약 배열의 원소들이 정렬이 되어있다면 이진탐색기법을 활용할 수 있다. 이 경우 연산 회수가 길이의 로그에 비례함을 알 수 있다. 왜냐면 한 번 수행할 때 마다 탐색해야할 데이터의 크기가 반으로 줄기 때문이다. 정확하게는 base가 2인 로그이지만 흔히 log로 표현한다. (밑이 10인 상용로그나 e인 자연로그는 아님을 주의)
- 검색: 일반적인 경우에는 O(n). 만약 원소들이 정렬이 되어있다면 O(log n)가 가능하다
2. Double Linked List - CAtlList, CList, std::list
설명이 필요없는 자료구조론의 교본; 더블 링크드 리스트. 배열과의 가장 다른 점은 원소가 연속적인 메모리가 아닌 포인터로 불연속적으로 저장된다는 점이다. 따라서 랜덤하게 접근이 불가능하며, ATL/MFC의 경우에는 POSITION이라는 iterator를, STL에서는 list::iterator 객체를 이용해서 접근해야한다. (따라서 STL의 소팅 알고리즘을 바로 적용할 수 없다. 소팅 알고리즘은 random access iterator를 요구하기 때문이다.)
- 삽입/삭제: 삽입을 하려면 앞/뒤의 노드에 대한 iterator가 필요하다. 따라서 이것을 구했다면 삽입은 상수시간 O(1)에 가능하다. 그러나 마치 배열 처럼 "몇 번째"에 넣기 위해서는 그에 해당하는 iterator를 구해야하고 결국 O(n)이 걸리게 된다. 따라서 이와 같은 경우가 많다면 배열을 사용해야 한다. 나의 경험상, 생각보다 더블 링크드 리스트가 반드시 필요한 경우는 많지 않았다.
- 검색: 당연히 O(n)
* 이 쯤에서 자료구조론 책에는 큐도 나오고, 스택도 나오고, deque도 나오지만 앞에 언급한 자료구조를 응용한 것에 불과하다.
3. Hash Table - CAtlMap, CMap, std::hash_map
해쉬 테이블은 key와 value 쌍을 저장하는 자료구조로서 DB의 기초가 되는 매우 중요한 자료구조이다. 해쉬 테이블의 개략적인 구조는 아래 그림과 같다. (구글에서 찾은 그림)
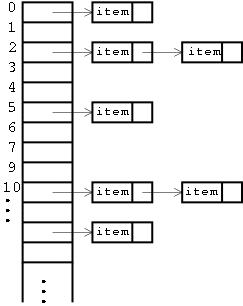
보다시피 세로로는 버킷(bucket)이라는 공간들이 배열 형태로 존재하고, 이 bucket에는 링크드 리스트가 주렁 주렁 달려있다. 해쉬 테이블의 가장 큰 장점은 검색이 매우 빠르다는 것이다. 해쉬 테이블에 자료의 삽입 및 검색은 다음 그림을 보자. 간단한 전화번호부 자료구조이다. (위키피디아에서 찾은 그림)

예를 들어, "John Smith"라는 key로 "+1-555-1234"라는 전화 번호를 저장하고 싶다. 먼저 해쉬 테이블은 주어진 key 값을 해쉬 함수 (hash function)을 통해 특정한 값으로 변환을 한다. 위 그림에서는 873이 되겠다. 그러면 바로 배열에 접근하듯이 873번 버킷에 접근을 한다. 만약 해쉬 값이 1000이 넘는다면 % modulo 연산자로 나머지 값을 취해 이 데이터가 위치할 버킷의 인덱스를 찾는다. 이 버킷에 이제 데이터를 싱글 링크드 리스트 형태로 저장을 하면 된다. 왜냐면, 위의 그림과 같이 "Sandra Dee"라는 key의 해쉬 값도 873으로 "John Smith"와 충돌(collision)이 일어나게 된다. 따라서 이런 충돌을 피하기 위해 같은 해쉬 값을 가지는 데이터는 리스트로 저장을 한다.
검색과 삭제의 방법도 같다. 주어진 키의 해쉬 값을 계산 한 뒤, 원하는 버킷으로 찾아가서, 버킷에 달려있는 데이터 노드와 비교를 하여 (선형 탐색) 원하는 데이터를 찾는 것이다.
따라서 검색에 필요한 시간 중 버킷까지 찾아가는 시간은 해쉬 테이블의 크기가 얼마가 되었든 동일하다. 그러나 만약 해쉬 테이블에 너무 많은 데이터가 있어 충돌이 많이 일어난 경우, 즉, 버킷에 긴 리스트가 달려있는 경우에는, 탐색하는데 시간이 소요되게 된다.
이론적인 해쉬 테이블의 검색 속도는 O(1+n/m)으로 표현한다. 여기서 m은 slot의 개수, n은 원소의 개수로 n/m은 흔히load factor로 표현이 된다. DB는 잘 몰라서 그런데, 흔히 0.7 ~ 1.2 정도의 값을 가지는 것이 좋을 것이다. 그러나 리스트는 평균적으로 그렇게 길지 않으므로 흔히 탐색은 상수시간 O(1)이 걸린다고 말한다. (정말로 최악의 경우에 모든 키의 해쉬 값이 하나로만 나온다면 검색 속도는 리스트와 같아진다.)
추가 및 삭제도 모두 상수시간 O(1)이 걸린다. 그림과 같이 주어진 이름으로 전화번호를 찾아야하는 사전과 같은 구조에서는 해쉬 테이블이 가장 좋다.
그러나 하나 주의해야할 것은, 해쉬 테이블에 저장된 데이터는 순서를 예측할 수 없다. 그림에서 해쉬 테이블에 저장된 모든 데이터를 출력한다고 할 때, 이는 정렬되지 않은 값이다. 왜냐면 주어진 키의 해쉬 값에 따라 정렬이 되는데 이는 일반적으로 예측할 수 없기 때문이다. 따라서 위의 그림에서 사람 이름으로 정렬해서 출력하고 싶다면, 어쩔 수 없이 모든 데이터를 한번 정렬를 해야한다.
4. Balanced Binary Search Tree(Red-Black Tree) - CRBMap, std::map (MFC 컬렉션은 없음)
역시 매우 중요한 자료구조. 균형잡힌(!) 이진 탐색 트리는 추가, 삭제, 검색을 모두 로그 시간 O(log n)에 수행할 수 있는 매우 우수한 자료구조이다. 비록 해쉬 테이블 상수 시간에 이루어지지는 않지만, 탐색 트리의 장점은 키 값들이 정렬이 되어있다는 것이다. 따라서 위의 전화번호부 예에서 사람 이름에 대해서 소팅을 많이 해야한다면, 이진 트리를 사용해야한다.
이진 트리는 아래와 같이 생긴 자료구조이다. 그러나 최악의 경우 모든 원소가 한 쪽에만 달려있다면, 이는 리스트와 전혀 다름이 없다.

따라서, 양쪽 노드의 개수를 "적절히" 분배를 해주는 것이 가장 중요하다. 만약 똑같이 분배가 되어있다면, 탐색 및 연산 작업이 로그 시간에 수행될 수 있다. 최대 트리의 높이만큼 순회하면 되므로 log 시간이 걸리는 것이다. 이렇게 연산 시간을 로그 시간이 될 수 있도록 보장하는 이진 트리를 Balanced Binary Search Tree라고 부른다. 여기에는 정말로 많은 자료구조가 있으며 해야할 얘기도 무척 많다. 그러나 대표적인 Red-Black Tree만 얘기해보자.

그림에서 보듯이, 각각의 노드에 빨강, 검정색의 속성을 추가한다. 그리고 빨간 노드의 자식은 모두 검정 노드여야한다와 같은 여러 속성을 정하고, 삽입/추가할 때 마다 이 속성이 유지되도록 보정을 해준다. (예: rotation) 그래서 노드가 균형을 유지하도록 한다. Red-Black Tree는 양쪽 노드의 깊이가 서로 두배 이상 차이가 나지 않음을 보장한다.
반면, AVL Tree라고 불리는 녀석은 양쪽 노드의 길이가 최대 하나 밖에 차이가 나지 않도록 한다. 훨씬 더 빡세게 균형을 맞춘다. 따라서 당연히 이 균형을 맞추는 보정 작업에 소요되는 시간이 Red-Black Tree보다 크다.
키와 데이터 쌍을 저장할 때, 검색이 가장 우선 순위라면 당연히 해쉬 테이블을 써야한다. 그러나 이 키 값들이 정렬이 되고 싶다면 Red-Black Tree가 가장 좋은 자료구조이다.
정리
위의 모든 내용을 정리한 아주 좋은 테이블이 MSDN 싸이트에 있다.
|
Shape |
Ordered? |
Indexed? |
Insert an element |
Search for specified element |
Duplicate elements? |
|
List |
Yes |
No |
Fast (constant time) |
Slow O(n) |
Yes |
|
Array |
Yes |
By int (constant time) |
Slow O(n) except if inserting at end, in which case constant time |
Slow O(n) |
Yes |
|
Map |
No |
By key (constant time) |
Fast (constant time) |
Fast (constant time) |
No (keys) Yes (values) |
|
Red-Black Map |
Yes (by key) |
By key O(log n) |
Fast O(log n) |
Fast O(log n) |
No |
|
Red-Black Multimap |
Yes (by key) |
By key O(log n) (multiple values per key) |
Fast O(log n) |
Fast O(log n) |
Yes (multiple values per key) |
| big O notation 알고리즘 2008.09.22 17:45 | 오이싫어 |
▶ logN
만약 입력 자료의 수에 따라 실행 시간이 logN의 관계를 만족한다면 N이 증가함에따라 실행 시간이 조금씩 늘어난다. 이 유형은 주로 커다란 문제를 일정한 크기를 갖는 작은 문제로 쪼갤 때 나타나는 유형이다.
log의 성질상 및(base)의 값에 따라 결과는 달라지지만 그렇게 크게 다르지는 않다. 예를 들어 N이 1000일 때 밑이 10이라면 결과는 3이 나오지만 밑이 2라면 약 10의 값을 가진다. 이 차이는 아주 작은 것이다. 이 유형의 알고리즘도 굉장히 바람직한 실행 시간을 갖는다.
성능이 좋은 검색 알고리즘은 대부분 logN의 수행 시간을 갖는다.
▶ N
입력 자료의 수에 따라 선형적으로 실행 시간이 걸리는 경우이다. 이는 입력 자료 각각에 일정 정도의 동일한 처리를 할 때 나타나는 경우이다. N이 두 배로 늘어나면 실행 시간도 두 배로 늘어난다. 이 유형도 납득할 만한 실행 시간을 갖는다.
▶ NlogN
이 유형은 커다란 문제를 독립적인 작은 문제로 쪼개어 각각에 대해 독립적으로 해결하고, 나중에 다시 그것들을 하나로 모으는 경우에 나타난다. N이 두 배로 늘어나면 실행 시간은 두 배보다 약간 더 많이 늘어난다.
성능이 좋은 정렬 알고리즘의 실행시간은 NlogN에 비례한다.
▶ N2
이 유형은 이중 루프 내에서 입력 자료를 처리하는 경우에 나타난다. N값이 큰 값이되면 실행 시간은 감당하지 못할 정도로 커지게 된다. 그래서 이 유형의 알고리즘은 많은 양의 입력 자료에 대해서는 사용이 부적절하다. N이 두 배로 늘어난다면 실행 시간은 네 배로 늘어난다.
▶ N3
이 유형은 앞의 유형과 비슷하게 입력 자료를 삼중 루프 내에서 처리하는 경우에 나타난다. N값이 커짐에 따라 실행 시간은 훨씬 더 커지게 된다. 역시 이 유형의 알고리즘은 다량의 입력 자료에 대해서는 부적절하며, 문제가 있는 알고리즘이 된다. N이 두배로 늘어난다면 실행 시간은 여덟 배로 늘어난다.
▶ 2N
입력 자료의 수가 늘어남에 따라 급격히 실행 시간이 늘어난다. 이 유형은 흔하지는 않지만 가끔씩 알고리즘을 처음 개발할 때 보인다. 하지만 이런 알고리즘은 대부분 더 좋은 성능의 알고리즘으로 개선된다. N이 두배로 늘어난다면 실행 시간은 제곱으로 늘어난다.
'각종 실기시험 자료실 > - 정보처리기사' 카테고리의 다른 글
| 한국정보통신기술협회(TTA) 2009~2010 표준용어들 (0) | 2011.04.27 |
|---|---|
| 최소비용신장트리구하기 알고리즘 동영상 강의 (0) | 2011.04.26 |
| 정렬 알고리즘(2)-선택정렬, (0) | 2009.01.27 |
| 각종 정렬 알고리즘 모음 (0) | 2009.01.27 |
| 2005년 4회 (10월 23일 시행) 정보처리기사 실기 기출문제 입니다. (0) | 2009.01.27 |